
Asked in MTX Group
AVL Tree Insertion Problem
Given an AVL tree, your task is to insert an element into the AVL Tree ensuring it remains balanced.
An AVL tree is a self-balancing binary search tree with the following properties:
- For every node, the nodes in its left subtree are less than the node, and nodes in the right subtree are greater than the node.
- The absolute difference between the height of the left subtree and the right subtree of any node is less than or equal to 1.
Read more about AVL Trees here.
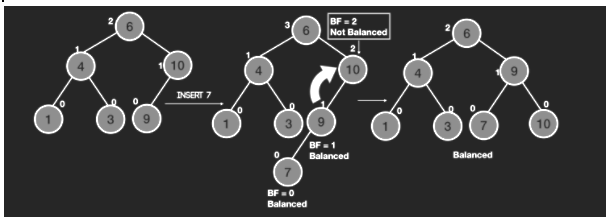
Example:
Input:
t = 1
level-order elements = 1 2 3 4 -1 5 6 -1 7 -1 -1 -1 -1 -1 -1
value to insert = 7
Output:
Returns the root node of the adjusted AVL tree
Constraints:
1 ≤ T ≤ 1001 ≤ N ≤ 3 * 103- The time limit is 1 second.
Note:
- Do not print anything; just return the root node of the AVL tree.
- The correctness of your implementation will be verified through in-order traversal of the final tree from the returned root node.
The input for each test case begins with a single integer 't' denoting the number of test cases. The first line of each test case provides the elements of the tree in level-order, separated by single spaces. The second line contains an integer value to be inserted. Use '-1' to denote a missing node.Output Format
For each test case, return the root node of the modified AVL tree after the element has been inserted.
AnswerBot
4mo
Insert an element into an AVL tree while maintaining balance.
Ensure the AVL tree remains balanced after insertion by performing rotations if necessary.
Update the height of each node after insertion to...read more
Help your peers!


Add answer anonymously...
Interview Questions Asked to Full Stack Developer at Other Companies
Top Skill-Based Questions for MTX Group Full Stack Developer
Web Development Interview Questions and Answers
250 Questions
Algorithms Interview Questions and Answers
250 Questions
Data Structures Interview Questions and Answers
250 Questions
JavaScript Interview Questions and Answers
250 Questions
Java Interview Questions and Answers
250 Questions
Software Development Interview Questions and Answers
250 Questions
Stay ahead in your career. Get AmbitionBox app


Trusted by over 1.5 Crore job seekers to find their right fit company
80 L+
Reviews
10L+
Interviews
4 Cr+
Salaries
1.5 Cr+
Users
Contribute to help millions
AmbitionBox Awards
Get AmbitionBox app













