
Asked in LinkedIn
Optimal BST Problem Statement
You are given a sorted array representing keys of a BST and an array of frequency counts showing how often each key is searched. Your task is to construct a binary search tree (BST) to minimize the total cost of searches.
The cost of searching is calculated as the frequency of a node multiplied by its level in the BST.
A BST is a binary tree where each node's key is greater than those in its left subtree and less than those in its right subtree.
Example:
Input:
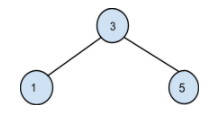
keys = [1, 3, 5]
Frequency = [3, 10, 7]
Output:
30
Explanation:
Construct various BSTs with given keys and frequencies and calculate the search cost. The BST with the lowest cost has a total cost of 30.
Constraints:
1 <= T <= 52 <= N <= 500 <= data <= 10^4
Input:
The first line of input contains an integer T, representing the number of test cases.
The first line of each test case contains an integer N, the number of elements in the BST.
The second line contains N sorted integers.
The third line contains N integers showing the frequency of each element.
Output:
For each test case, output the minimum total cost of constructing the BST on a new line.
Note:
1. The given BST will not contain duplicate keys.
2. Implementation only: printing is handled separately.

Construct a BST with minimum search cost based on keys and frequencies.
Create a recursive function to construct the BST by considering all possible root nodes.
Calculate the cost for each possible BST ...read more


Top Software Developer Interview Questions Asked at LinkedIn
Interview Questions Asked to Software Developer at Other Companies
Top Skill-Based Questions for LinkedIn Software Developer


Reviews
Interviews
Salaries
Users













