Validate BST
You have been given a binary tree of integers with N number of nodes. Your task is to check if that input tree is a BST (Binary Search Tree) or not.
A binary search tree (BST) is a binary tree data structure which has the following properties.
• The left subtree of a node contains only nodes with data less than the node’s data.
• The right subtree of a node contains only nodes with data greater than the node’s data.
• Both the left and right subtrees must also be binary search trees.
Example :
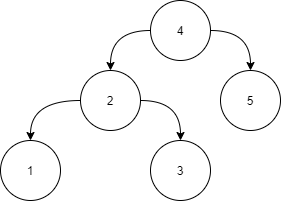
Answer :
Level 1:
All the nodes in the left subtree of 4 (2, 1, 3) are smaller
than 4, all the nodes in the right subtree of the 4 (5) are
larger than 4.
Level 2 :
For node 2:
All the nodes in the left subtree of 2 (1) are smaller than
2, all the nodes in the right subtree of the 2 (3) are larger than 2.
For node 5:
The left and right subtrees for node 5 are empty.
Level 3:
For node 1:
The left and right subtrees for node 1 are empty.
For node 3:
The left and right subtrees for node 3 are empty.
Because all the nodes follow the property of a binary search tree, the above tree is a binary search tree.
Input Format :
The first line contains an integer 'T', which denotes the number of test cases or queries to be run. Then the test cases follow.
The first line of input contains the elements of the tree in the level order form separated by a single space.
If any node does not have a left or right child, take -1 in its place. Refer to the example below.
Example :
Elements are in the level order form. The input consists of values of nodes separated by a single space in a single line. In case a node is null, we take -1 in its place.
For example, the input for the tree depicted in the below image would be :
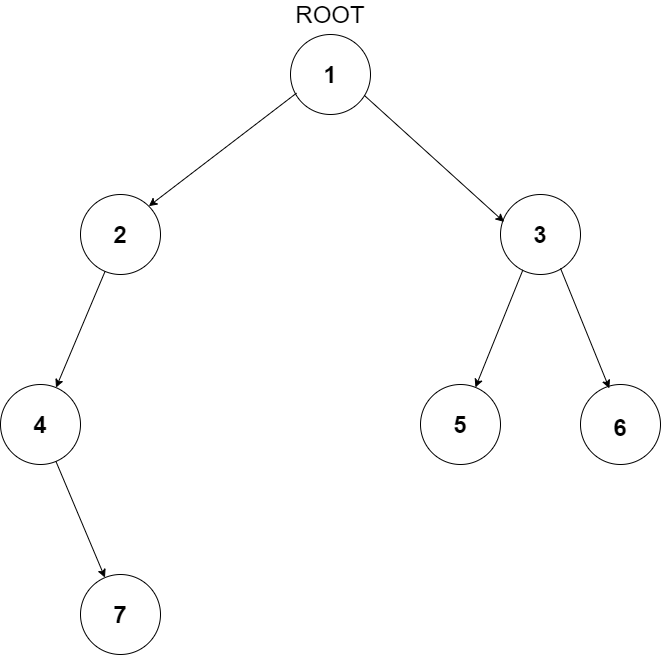
1
2 3
4 -1 5 6
-1 7 -1 -1 -1 -1
-1 -1
Explanation :
Level 1 :
The root node of the tree is 1
Level 2 :
Left child of 1 = 2
Right child of 1 = 3
Level 3 :
Left child of 2 = 4
Right child of 2 = null (-1)
Left child of 3 = 5
Right child of 3 = 6
Level 4 :
Left child of 4 = null (-1)
Right child of 4 = 7
Left child of 5 = null (-1)
Right child of 5 = null (-1)
Left child of 6 = null (-1)
Right child of 6 = null (-1)
Level 5 :
Left child of 7 = null (-1)
Right child of 7 = null (-1)
The first not-null node (of the previous level) is treated as the parent of the first two nodes of the current level. The second not-null node (of the previous level) is treated as the parent node for the next two nodes of the current level and so on.
The input ends when all nodes at the last level are null (-1).
Note :
The above format was just to provide clarity on how the input is formed for a given tree.
The sequence will be put together in a single line separated by a single space. Hence, for the above-depicted tree, the input will be given as:
1 2 3 4 -1 5 6 -1 7 -1 -1 -1 -1 -1 -1
Output Format :
For each test case, print ‘true’ if the binary tree is a BST, else print ‘false’.
Output for every test case will be denoted in a separate line.
Note :
You are not required to print anything explicitly. It has already been taken care of. Just implement the function.
Constraints :
1 <= T <= 100
1 <= N <= 5000
-10^6 <= data <= 10^6 and data != -1
where N is the number of nodes in the tree, T represents the number of test cases, and ‘data’ denotes data contained in the node of the binary tree.
Time Limit: 1 sec
CodingNinjas
author
2y
BST property
The approach is based on the fact that the value of each node in a BST is greater than the value of all the nodes in the left subtree and smaller than the value of all the nodes in the rig...read more
CodingNinjas
author
2y
Inorder Traversal
The main idea behind this approach is that if an inorder traversal is performed on a binary search tree, then the elements are in ascending order.
- While performing the traversal, keep...read more
Help your peers!
Add answer anonymously...
Popular interview questions of Software Developer Intern
>
SpeedLabs Software Developer Intern Interview Questions
Stay ahead in your career. Get AmbitionBox app

Helping over 1 Crore job seekers every month in choosing their right fit company
65 L+
Reviews
4 L+
Interviews
4 Cr+
Salaries
1 Cr+
Users/Month
Contribute to help millions
Get AmbitionBox app