Topological Sort Problem Statement

You are given a directed acyclic graph (DAG). Your task is to perform topological sorting of the graph and return any valid ordering.

Explanation:

A directed acyclic graph is a graph without cycles where edges have a direction. In a topological sort of the DAG, every directed edge from node U to node V ensures that U comes before V in the ordering.

Example:

Consider the following DAG:

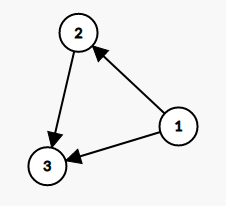
One possible topological sorting of this graph is:

1 2 3

Input:

The first line contains an integer ‘T’ for the number of test cases.
Each test case starts with two integers ‘N’ (number of nodes) and ‘M’ (number of edges).
The following ‘M’ lines each contain a pair of integers ‘U’ and ‘V’, indicating a directed edge from ‘U’ to ‘V’.

Output:

For each test case, output a line with ‘N’ space-separated integers that represent a topological sort of the graph. Each test case's result should be printed on a new line.

Constraints:

• 1 <= T <= 100
• 1 <= N <= 5000
• 0 <= M <= min(5000, (N*(N-1))/2)
• 1 <= U, V <= N and U != V

Note: You don’t need to print the output, only implement the function to return the answer.