Bellman Ford Shortest Path Problem

Given a directed weighted graph comprised of vertices labeled 1 to N and M edges, where each edge connects two nodes u and v with a weight w representing the distance between them.

Your task is to calculate the shortest path length from a specified source vertex (src) to a destination vertex (dest). The graph may contain edges with negative weights.

Example:

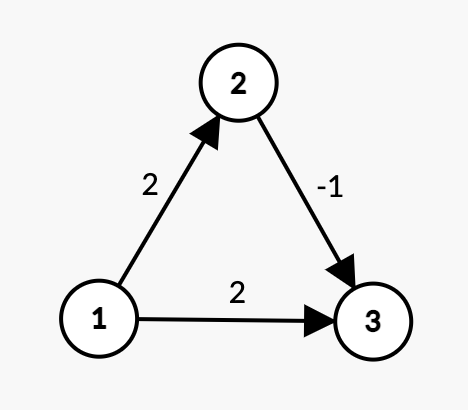
Input:

3 3 1 3
1 2 2
1 3 2
2 3 -1

Output:

1

Explanation:

In the given graph, the shortest path from vertex 1 to vertex 3 is 1->2->3 with a total weight of 2 - 1 = 1.

Constraints:

• The graph does not have self-loops or multiple edges.
• No negative weight cycles are present in the graph.
• 1 <= T <= 10 (number of test cases)
• 1 <= N <= 50 (number of vertices)
• 1 <= M <= 300 (number of edges)
• 1 <= src, dest <= N (source and destination vertex)
• 1 <= u,v <= N
• -10^5 <= w <= 10^5 (edge weight)
• Time Limit: 1 second

Input:

The first line contains an integer ‘T’ representing the number of test cases.
Each test case starts with four space-separated integers ‘N’, ‘M’, ‘src’, and ‘dest’, representing the number of vertices, number of edges, source vertex, and destination vertex.

Output:

For each test case, return an integer representing the shortest path length from ‘src’ to ‘dest’. If no path is available, return 10^9.

Note:

You do not need to print anything; this will be handled for you. Focus on implementing the function to find the solution.