Bellman Ford Shortest Path Problem
Given a directed weighted graph comprised of vertices labeled 1 to N and M edges, where each edge connects two nodes u and v with a weight w representing the distance between them.
Your task is to calculate the shortest path length from a specified source vertex (src) to a destination vertex (dest). The graph may contain edges with negative weights.
Example:
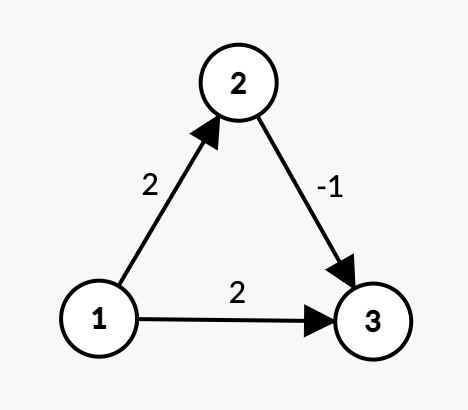
Input:
3 3 1 3
1 2 2
1 3 2
2 3 -1
Output:
1
Explanation:
In the given graph, the shortest path from vertex 1 to vertex 3 is 1->2->3 with a total weight of 2 - 1 = 1.
Constraints:
- The graph does not have self-loops or multiple edges.
- No negative weight cycles are present in the graph.
1 <= T <= 10(number of test cases)1 <= N <= 50(number of vertices)1 <= M <= 300(number of edges)1 <= src, dest <= N(source and destination vertex)1 <= u,v <= N-10^5 <= w <= 10^5(edge weight)- Time Limit: 1 second
Input:
The first line contains an integer ‘T’ representing the number of test cases.
Each test case starts with four space-separated integers ‘N’, ‘M’, ‘src’, and ‘dest’, representing the number of vertices, number of edges, source vertex, and destination vertex.
Output:
For each test case, return an integer representing the shortest path length from ‘src’ to ‘dest’. If no path is available, return 10^9.
Note:
You do not need to print anything; this will be handled for you. Focus on implementing the function to find the solution.

AnswerBot
4mo
Bellman Ford algorithm is used to find the shortest path in a graph with negative weights.
Initialize distances from source to all vertices as infinity, and distance to source as 0.
Relax all edges V-1 ...read more
Help your peers!


Add answer anonymously...
Qualcomm Software Developer interview questions & answers
A Software Developer was asked Q. Design and implement a hash map data structure.
A Software Developer was asked Q. Tell me more about your domain knowledge of the ARM processor architecture.
A Software Developer was asked Q. How can you swap two numbers without using a third variable?
Popular interview questions of Software Developer
A Software Developer was asked Q1. Design and implement a hash map data structure.
A Software Developer was asked Q2. Tell me more about your domain knowledge of the ARM processor architecture.
A Software Developer was asked Q3. How can you swap two numbers without using a third variable?
Stay ahead in your career. Get AmbitionBox app


Trusted by over 1.5 Crore job seekers to find their right fit company
80 L+
Reviews
10L+
Interviews
4 Cr+
Salaries
1.5 Cr+
Users
Contribute to help millions
AmbitionBox Awards
Get AmbitionBox app












