Print Nodes at Distance K From a Given Node
You are given an arbitrary binary tree, a node of the tree, and an integer 'K'. You need to find all such nodes which have a distance K from the given node and return the list of these nodes.
Distance between two nodes in a binary tree is defined as the number of connections/edges in the path between the two nodes.
Note:
1. A binary tree is a tree in which each node has at most two children.
2. The given tree will be non-empty.
3. The given tree can have multiple nodes with the same value.
4. If there are no nodes in the tree which are at distance = K from the given node, return an empty list.
5. You can return the list of values of valid nodes in any order. For example if the valid nodes have values 1,2,3, then you can return {1,2,3} or {3,1,2} etc.
Input Format:
The first line of the input contains an integer T, denoting the number of test cases to run.
The first line of each test case will contain the values of the nodes of the tree in the level order form ( -1 for NULL node). Refer to the example below for further explanation.
The second line of each test case contains the value of the target node.
The third and the last line of each test case contains the integer K denoting the distance at which nodes are to be found.
Example:
Consider the binary tree:
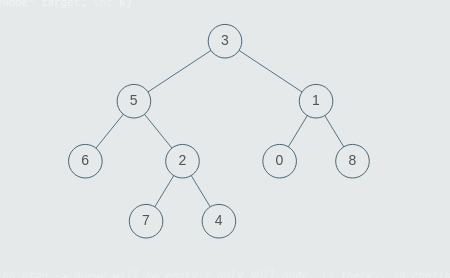
The input for the tree depicted in the above image would be :
3
5 1
6 2 0 8
-1 -1 7 4 -1 -1 -1 -1
-1 -1 -1 -1
Explanation :
Level 1 :
The root node of the tree is 3
Level 2 :
Left child of 3 = 5
Right child of 3 = 1
Level 3 :
Left child of 5 = 6
Right child of 5 = 2
Left child of 1 = 0
Right child of 1 = 8
Level 4 :
Left child of 6 = null (-1)
Right child of 6 = null(-1)
Left child of 2 = 7
Right child of 2 = 4
Left child of 0 = null (-1)
Right child of 0 = null (-1)
Left child of 8 = null (-1)
Right child of 8 = null (-1)
Level 5 :
Left child of 7 = null (-1)
Right child of 7 = null (-1)
Left child of 4 = null (-1)
Right child of 4 = null (-1)
The first not-null node (of the previous level) is treated as the parent of the first two nodes of the current level. The second not-null node (of the previous level) is treated as the parent node for the next two nodes of the current level and so on.
The input ends when all nodes at the last level are null (-1).
Output Format :
For each test case, print the values of all nodes at distance = K, from the given target node.
Note:
You do not need to print anything, it has already been taken care of. Just implement the given function.
Constraints:
1 <= T <= 100
1 <= N <= 3000
0 <= K <= 3000
0 <= nodeValue <= 3000
Where nodeValue donates the value of the node.
Time Limit: 1 sec
AnswerBot
1y
The task is to find all nodes in a binary tree that are at a distance K from a given node.
Traverse the binary tree to find the given node
From the given node, perform a depth-first search to find all n...read more
CodingNinjas
author
2y
Recursion can be applied in this problem. Maintain a variable k to store the distance. If the node is null or k <0 , return. If k==0, this is the node at distance k from the root node. So, print it. M...read more
CodingNinjas
author
2y
DFS
- Create a map to store the parent of each node in the tree, Traverse the tree recursively (via depth-first search), at each step if the current node is not NULL. Store its parent in the map, then tr...read more
CodingNinjas
author
2y
Insertion with Depth Calculation.
- A general idea for this approach is that if from the root, the target lies in its left branch at distance ‘X’, then all nodes in its right branch at distance ‘K’ - ‘X’...read more
Add answer anonymously...
Top Info Edge Software Developer interview questions & answers
Popular interview questions of Software Developer
Top HR questions asked in Info Edge Software Developer
Stay ahead in your career. Get AmbitionBox app

Helping over 1 Crore job seekers every month in choosing their right fit company
65 L+
Reviews
4 L+
Interviews
4 Cr+
Salaries
1 Cr+
Users/Month
Contribute to help millions
Get AmbitionBox app