Snake and Ladder Problem Statement
Given a 'Snake and Ladder' board with N rows and N columns, where positions are numbered from 1 to (N*N) starting from the bottom left, alternating direction each row, find the minimum number of dice throws required to reach the last cell. The dice has six faces, and you control its outcome.
Example:
For a (6 x 6) board, numbers are placed as shown in the image:
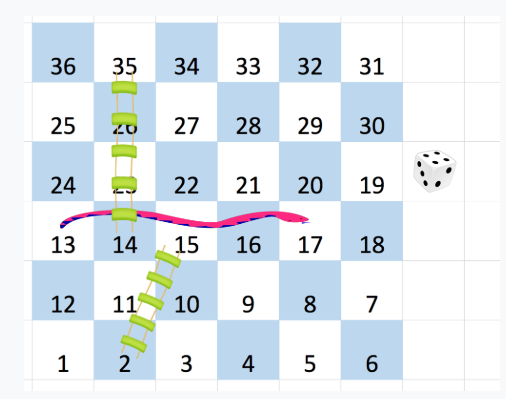
Explanation:
You start on square 1 at the last row and first column. On square 'X', you can opt to move to a square 'S' being 'X+1', 'X+2', ..., 'X+6', as long as 'S' is ≤ N*N. If 'S' hosts a snake or ladder, you are transported to board[i][j]. A board square at [i][j] encases "Snake or Ladder" mechanics if board[i][j] ≠ -1.
Input:
N
board[0][0] board[0][1] ... board[0][N-1]
board[1][0] board[1][1] ... board[1][N-1]
...
board[N-1][0] board[N-1][1] ... board[N-1][N-1]Output:
Minimum number of throws to reach the last board cell, or -1 if unreachable.Constraints:
- 1 <= N <= 102
- 1 <= board[i][j] <= N*N or board[i][j] = -1
Note:
- '-1' signifies absence of any Snake or Ladder on the square.
- Snakes and Ladders can only be utilized once per move. Moving from one to the start of another does not continue your journey.

Find the minimum number of dice throws required to reach the last cell on a 'Snake and Ladder' board.
Use Breadth First Search (BFS) algorithm to find the shortest path from start to end cell.
Keep trac...read more




Reviews
Interviews
Salaries
Users













